カテゴリー: 【数学の話題】

　s-800 数学のいずみ_top.jpg
　—– * —– * –

　検索を繰り返していたとき「数学のいずみ」が目に留まり久し振りに訪れてみました。「ネットワーク型教材データベース」と銘打って実践研究やレポート・数学コンテストなど，指導法の研究や教材開発などなど盛りだくさんです。「数学の小手技」や「メイくる数学」・「プリント倉庫」などもあり，全貌が捉えられないくらい広い世界が広がっています。とても勉強になります。とても刺激になります。ぜひ繋いでみてください。

　　　数学のいずみ　http://izumi-math.jp

　—– * —– * –

　著者別索引・単元別索引もついています。今回の中村文則先生のレポート

　　『■ 折り紙で開く万華の彩り…折ってつくる折り紙カライドサイクル!!　』

を著者別索引から探すこともできますが中村先生の索引ページだけでも1000行を超えタイトルも150以上はあるものと思われます。

　■ 折り紙カライドサイクル

　　　http://izumi-math.jp/F_Nakamura/kaleidocycles.pdf

　　　pdfの内容を読むにはリンクからが最適と思われますが，11ページに及ぶレポートを1ページにまとめてみるとこんな感じです。

　　　　　　　　s-640 数学のいずみ_11p-in1-1.jpg

　—– * —– * —–

　9ページに蝶が舞う型紙がありましたので作ってみました。

　　s-800 蝶.jpg

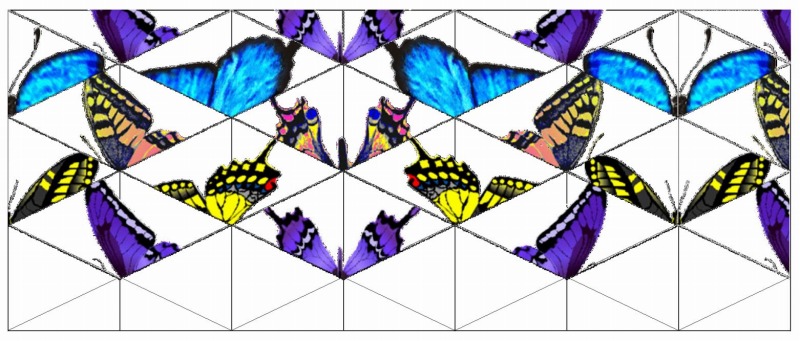
　　s-1024 蝶が舞うからいどさいくる４面.jpg

【数学の話題】